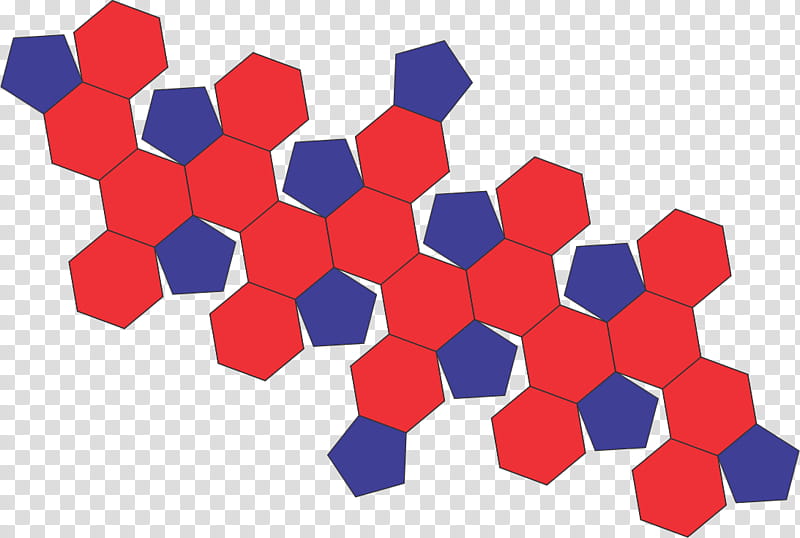
Rhombic Triacontahedron Net

And heres a compound of the rhombic triacontahedron in grey and its dual. The white triacontahedron was made from readily available 5x8 index cards and is very sturdy. Calculations at a rhombic triacontahedron the dual body of the icosidodecahedrona rhombic triacontahedron is a polyhedron with rhombic faces those have angles of 634350 and 1165650.
rhombic triacontahedron net

Acceptance Domain In The Form Of A Rhombic Triacontahedron For The

Rhombic Triacontahedron 3d Cad Model Library Grabcad

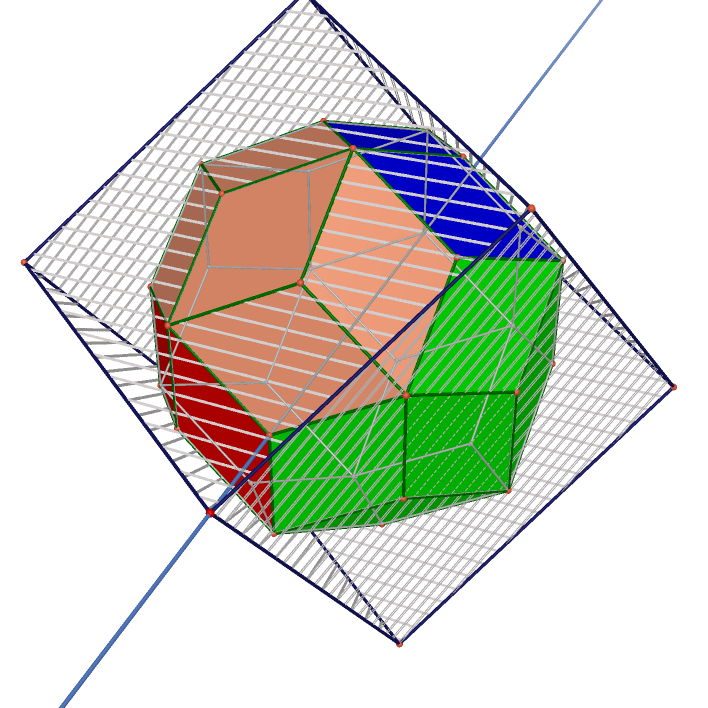
Motivation Of Net Of Rhombic Triacontahedron With 6 Colors

One is this compound of an icosahedron and its dual the dodecahedron.

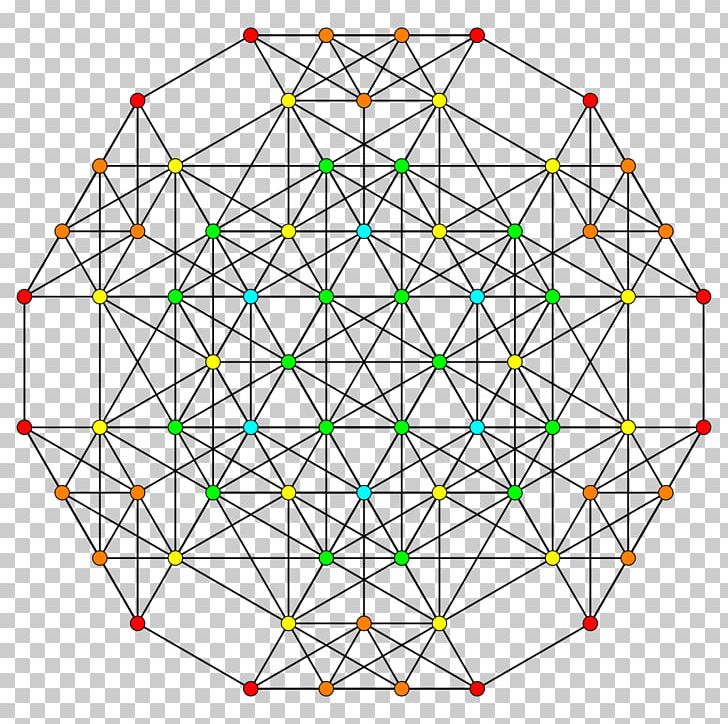
Rhombic triacontahedron net. Polyhedra which share the same set of vertices. This is same shape as a d30. It has twenty vertices with three edges and twelve vertices with five edges. It slightly resembles an inflated rhombic triacontahedronif one replaces each face of the rhombic triacontahedron with a.

The rhombic triacontahedron is a combined icosahedron dodecahedron dual so it is not surprising to see so many relationships based on the division in mean and extreme ratio. The pink triacontahedron was made from 55x85 sheets aspect ratio of 1711 and is too loose to stay together. The rhombic triacontahedron has many facetings ie. If the edge length of a rhombic triacontahedron is a surface area volume the radius of an inscribed sphere tangent to each of the rhombic triacontahedrons faces and midradius which touches the middle of each edge are.

Using golden rhombi you can make this pretty cool 30 sided spheroid to impress your friends. The rhombic triacontahedron is somewhat special in being one of the nine edge transitive convex polyhedra the others being the five platonic solids the cuboctahedron the icosidodecahedron and the rhombic dodecahedron. The multicolored triacontahedron was made from sheets cut to 425x2625 aspect ratio of 3421 and is very tight. Posts about rhombic triacontahedron written by robertlovespi.

The rhombic triacontahedron is also interesting in that its vertices include the arrangement of four platonic solids. The plane of each face is perpendicular to the center of the rhombic triacontahedron and is located at the same distance. In geometry a disdyakis triacontahedron hexakis icosahedron decakis dodecahedron or kisrhombic triacontahedron is a catalan solid with 120 faces and the dual to the archimedean truncated icosidodecahedronas such it is face uniform but with irregular face polygons. The rhombic triacontahedron contains all of the properties of the icosahedron and all of the properties of the dodecahedron and it tells us the proper nesting order of the 5 platonic solids.

Where f is the golden ratio. One nice thing about these two polyhedra is that one of them the rhombic triacontahedron can be used repeatedly as a building block to build the other one the icosidodecahedron.